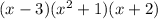Question

Y=x^4-x^3-5x^2-x-6
Show steps

Answer 1

The roots (zeros) are the x values where the graph intersects the x-axis. To find the roots (zeros), replace y with 0 and solve for x. x= i, −i, 3,−2

Explanation:

Answer 2

`(x-3)({x}^(2)+1)(x+2)`

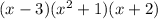
Explanation:

1) Factor
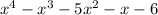`x^4 - x^3 - 5x^2 - x - 6` using Polynomial Division.

1 - Factor the following.

`x^4 - x^3 - 5x^2 - x - 6`

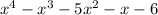
2 - First, find all factors of the constant term 6.

`1, 2, 3, 6`

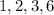
3 - Try each factor above using the Remainder Theorem.

Substitute 1 into x. Since the result is not 0, x-1 is not a factor..

`1^4 - 1^3 - 5 * 1^2 - 1 - 6 = - 12`

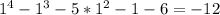
Substitute -1 into x. Since the result is not 0, x+1 is not a factor..

`( - 1 ) ^ 4 - ( - 1 ) ^ 3 - 5 ( - 1 ) ^ 2 + 1 - 6 = - 8`

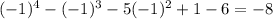
Substitute 2 into x. Since the result is not 0, x-2 is not a factor..

`{2}^(4)-{2}^(3)-5* {2}^(2)-2-6 = -20`

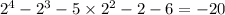
Substitute -2 into x. Since the result is 0, x+2 is a factor..

`{(-2)}^(4)-{(-2)}^(3)-5{(-2)}^(2)+2-6 = 0`

⇒
`x+2`

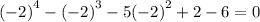
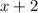
4 - Polynomial Division: Divide
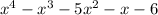`{x}^(4)-{x}^(3)-5{x}^(2)-x-6` by
`x+2`

`x^3`
`-3x^2`
`x`
`-3`

--------------------------------------------------------------

`x+2` |
`x^4`
`-x^3`
`-5x^2`
`-x`
`-6`

`x^4`
`2x^3`

------------------------------------------------------------

`-3x^3`
`-5x^2`
`-x`
`-6`

`-3x^3`
`-6x^2`

---------------------------------------

`-3x`
`-6`

`-3x`
`-6`

---------------

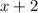
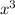
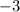
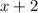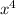
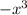
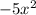
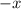
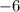
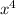
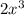
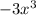
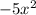
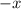
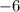
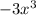
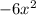
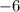
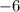
5 - Rewrite the expression using the above.

`{x}^(3)-3{x}^(2)+x-3`

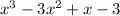
2) Factor out common terms in the first two terms, then in the last two terms.

`({x}^(2)(x-3)+(x-3))(x+2)`

3) Factor out the common term
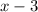`x-3`.

`(x-3)({x}^(2)+1)(x+2)`