Answer:
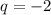
Explanation:
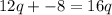
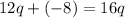
Start by getting rid of the addition sign, as a positive multiplied by a negative is negative:

Subtract
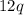 from both sides of the equation:
from both sides of the equation:
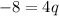
Divide both sides of the equation by the coefficient of
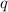 , which is
, which is
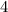 :
:
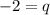
or
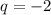
_
Check your by substituting the solved
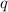 value in to the initial equation:
value in to the initial equation:
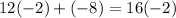
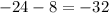

Since both sides of the equation are equal, our answer is correct!