Answer:
The sum of the first 9 terms in the geometric series is 127.75
Explanation:
In the geometric series, there is a constant ratio between each two consecutive numbers
Examples:
5, 10, 20, 40, 80, ………………………. (×2)
5000, 1000, 200, 40, …………………………(÷5)
General term (nth term) of a Geometric series is
a1 = a, a2 = ar, a3 = ar², a4 = ar³, ..........
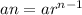, where
a is the first term
r is the constant ratio between each two consecutive terms
The sum of the first n terms of a Geometric series is calculated by this rule
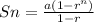
Let us solve the question
∵ The geometric series is 64, 32, 16, .......................
∴ a = 64
∴ r = 32 ÷ 64 = 0.5
→ We need to find the sum of the first 9 terms
∴ n = 9
→ Substitute these values on the formula of the sum above
∴
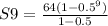
→ use the calculator to find the answer
∴ S9 = 127.75
∴ The sum of the first 9 terms in the geometric series is 127.75