Answer:
The first five terms are 2,
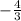 ,
,
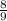 ,
,
 ,
,

Explanation:
In the geometric sequence, there is a constant ratio between each two consecutive numbers
Examples:
5, 10, 20, 40, 80, ………………………. (×2)
5000, 1000, 200, 40, …………………………(÷5)
General term (nth term) of a Geometric sequence is:
a1 = a, a2 = ar, a3 = ar², a4 = ar³, ..........
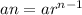 , where
, where
a is the first term
r is the constant ratio between each two consecutive terms
Let us solve the question
∵ A sequence has a first term of 2 and a constant ratio of

∴ This is a geometric sequence, where
- a = 2
- r =

→ We need to find the first 5 terms
∴ n = 5
∵
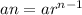
∵ At n = 1, First term = a
∴ The first term = 2
∵ At n = 2,
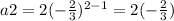
∴ The second term =
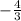
∵ At n = 3,

∴ The third term =
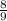
∵ At n = 4,
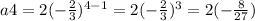
∴ The fourth term =

∵ At n = 5,
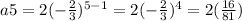
∴ The fourth term =

∴ The first five terms are 2,
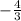 ,
,
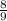 ,
,
 ,
,
