Question

What is the essence of calculus?
*friendship​

Answer 1

Differential Calculus, or Differentiation

If we have a function of one variable, ie of the form
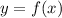`y=f(x)`, then in its most basic form differentiation is the study of how a small change in one variable
`x` affects the other variable
`y`.

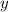As an real life example, consider the average speed of a moving car:

average speed = distance travelled/ time taken

Obviously, this is an average by definition, but if there existed a formal mathematical link between distance and time, could we build a function that would tell us the instantaneous velocity at every given moment? The study of differential calculus gives strategies for calculating the ratio of a little change in distance to a small change in time, and then calculating the real instantaneous speed by making the small change infinitely small.

Similarly if we wanted to find the gradient of the tangent to a curve at some particular point
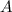`A` we would estimate the gradient by using a chord to a nearby point
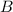`B`. As we move this nearby point
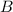`B` closer to the tangent point
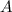`A` the slope of the chord approaches the slope of the tangent with more and more accuracy. Again differential calculus provides techniques for us to make the point
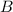`B` infinitesimally close to the point
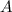`A` o that we can calculate the actual gradient of the tangent.

Integral Calculus, or Integration

Suppose we wanted to calculate the area under a curve,
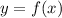`y=f(x)`, bounded the
`x` =axis, and two points
`a` and
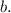`b.` We could start by splitting the interval
`[a,b]` into
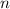`n` regular strips, and estimating the area under the curve using trapezia (this is the essence of the trapezium rule which provides an estimate of such an area). If we increase
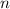`n` then generally we would hope for a better approximation. The study of integration provides techniques for us to take an infinitely large number of infinitesimally small strips to gain an exact solution.

The Fundamental Theorem of Calculus

Given the above two notions, it would appear that there is no connection between them at first., The Fundamental Theorem of Calculus, on the other hand, is a theorem that connects the rate of change of the area function (which determines the area under a curve) to the function itself. In other words, the area function's derivative equals the function itself.

Visual for Fundamental Theorem of Calculus for integrals:

`\int\limits^b_af {(x)} \, dx =F(b)-F(a).`

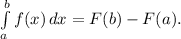
where F is an antiderivative of
`f`

Physics, Chemistry, all engineering sciences, statistics, economics, finance, biology, computer science, linguistics, to name but a few, are all areas that would be a desert without the use of calculus.

Leibnitz and Newton worked to define the velocity of a planet moving on a curved trajectory. That was not possible without calculus, and both had to invent differential calculus. Differential calculus allows to compare quantities along a curve, and thus their time rate of change.

All of classical physics can be summarized in this operation. Given second derivative (which is Force/mass), find the position as a function of time. This process is called integration. Half of calculus is made with integration, the other half with derivation. All of classical physics rests on these two parts of the calculus.

Quantum mechanics, quantum field theory, electromagnetism, fluid mechanics all use integration and derivation and much more. I rest my case. I hope this helps you gauge the place that calculus occupies in science.

Answer 2

so what i think is that *friendship​Step-by-step explanation: