Answer:
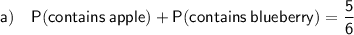

c) Not mutually exclusive events
Explanation:
From inspection of the Venn diagram:
- Total number of smoothies = 12 + 3 + 7 + 8 = 30
- Number of smoothies containing Apple = 12 + 3 = 15
- Number of smoothies containing Blueberry = 3 + 7 = 10
- Number of smoothies containing both Apple and Blueberry = 3
- Number of smoothies not containing Apple or Blueberry = 8
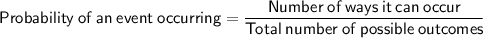
Let A = contains apple
Let B = contains blueberry
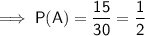
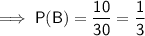
Part (a)

Part (b)
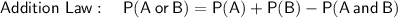
Given:
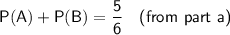


Or, we can simply read P(contains apple or blueberry) from the Venn diagram.
P(A or B) is the total of the numbers inside the circles divided by the total number of smoothies:
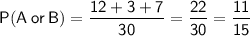
Part (c)
For two events, A and B, where A and B are mutually exclusive:
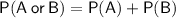
Given:
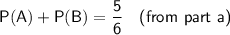
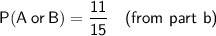
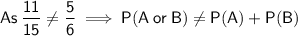
Therefore, choosing a smoothie containing apple and choosing a smoothie containing blueberry are NOT mutually exclusive events.