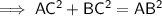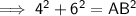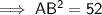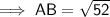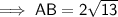Answer:
1) BC = 6
2) B = 33.7° (nearest tenth)
3)
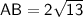
Explanation:
Trigonometric ratios
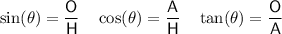
where:
 is the angle
is the angle- O is the side opposite the angle
- A is the side adjacent the angle
- H is the hypotenuse (the side opposite the right angle)
Question 1
Given:
- Angle = A
- Side opposite angle = BC
- Side adjacent angle = AC = 4
Substituting the values into the tan ratio:
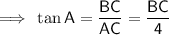
Given:
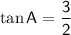
Therefore:
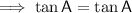


Question 2
Given:
- Angle = B
- Side opposite angle = AC = 4
- Side adjacent angle = BC = 6
Substituting the values into the tan ratio and solving for B:



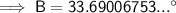
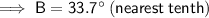
Question 3
Pythagoras’ Theorem

(where a and b are the legs, and c is the hypotenuse, of a right triangle)
Given:
- a = AC = 4
- b = BC = 6
- c = AB
Substituting the values into the formula and solving for AB: