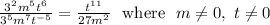Problem 1
Answer:
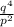
This is the fraction of
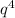 over top
over top
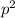
----------------------
Step-by-step explanation:
The
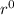 term becomes 1 since raising any nonzero value to the 0 exponent is 1.
term becomes 1 since raising any nonzero value to the 0 exponent is 1.
So
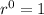 as long as r is nonzero.
as long as r is nonzero.
The negative exponent over the variable q will mean we apply the reciprocal to make that exponent positive. Meaning that
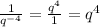
The
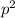 term stays as it is.
term stays as it is.
============================================================
Problem 2
Answer: 4
----------------------
Step-by-step explanation:
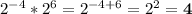
The exponent rule used here is
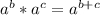 . You add the exponents together when multiplying exponential expressions of the same base.
. You add the exponents together when multiplying exponential expressions of the same base.
============================================================
Problem 3
Answer:
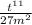
This is one single fraction with
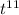 over top
over top
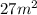
----------------------
Step-by-step explanation:
The rule we use is
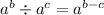 which is similar to the last rule, but now we're dividing the terms and subtracting the exponents. The bases must be the same.
which is similar to the last rule, but now we're dividing the terms and subtracting the exponents. The bases must be the same.
With that rule in mind we can say:
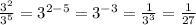
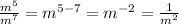
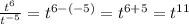
which when put together forms this
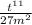
In other words,