Question

An "extreme" pogo stick utilizes a spring whose uncompressed length is 46 cm and whose force constant is 1.4 x 104 N/m. A 60-kg person is jumping on the pogo stick, compressing the spring to a length of only 5.0 cm at the bottom of their jump. Which is the upward acceleration of the person at the moment the spring reaches its greatest compression at the bottom of their jump?

a. 96 m/s^2
b. 86 m/s^2
c. 976 m/s^2
d.860 m/s^2

Answer 1

B.
`86\,(m)/(s^(2))`

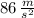
Explanation:

From Newton's Laws of Motion, the spring is compressed against effects of weight of the person and as sping force is a restitutive force, the net force experimented by person is different from zero. By applying Second Newton's Law, we get this equation of equilibrium on person:

`\Sigma F = k\cdot \Delta x -m\cdot g = m\cdot a` (Eq. 1)

Where:

`k` - Spring constant, measured in newtons per meter.

`\Delta x` - Change in the length of spring, measured in meters.

`m` - Mass of the person, measured in meters.

`g` - Gravitational acceleration, measured in meters per square second.

`a` - Net acceleration of the person, measured in meters per square second.

Now we proceed to clear net acceleration:

`a = (k)/(m)\cdot \Delta x -g`

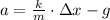
If we know that
`k = 1.4* 10^(4)\,(N)/(m)`,
`m = 60\,kg`,
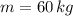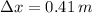`\Delta x = 0.41\,m` and
`g = 9.807\,(m)/(s^(2))`, the acceleration of the person when spring reaches its greatest compression at the bottom of their jump is:

`a = (1.4* 10^(4)\,(N)/(m) )/(60\,kg) \cdot (0.41\,m)-9.807\,(m)/(s^(2))`

`a = 85.859\,(m)/(s^(2))`

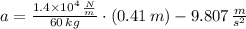
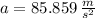
Which corresponds to option B.