Question

Someone answered it incorrectly, so please check image.

Answer 1

Answer: A 1. Linear because it goes up by 100 evenly

A. 2. Exponential because if you look it goes up rapidly and in no pattern .

B. 1. 1300*n= 2100

B. 2. 1331*n=F?

C. If she chooses option 2 she with get a good amount of money more than option 1.

hope this helps

Answer 2

Part A)

Option 1 is linear; Option 2 is exponential.

Part B)

`f(n)_1=100n+1000\\f(n)_2=1000(1.1)^n`

Part C)

After 20 years, Option 1 yields $3000.

After 20 years, Option 2 yields approximately $6727.50.

Yes, there is a significant difference. Melinda should invest using Option 2.

Explanation:

We know that Belinda invested a total of $1000. We also have a table showing the value of her investment.

Part A)

First, let's examine the table for Option 1. We can see that for each year after the deposit, the investment increases by $100. Since Option 1 increases by a constant rate of $100 per year, Option 1 is linear.

For Option 2, we can see that the amount added each year is not constant. For the first year, the investment earned a total of $1100 - $1000 = $100. However, for the second year, the investment earned $1210 - $1100 = $110. And, similarly, for the third year, the investment earned $1331 - $1210 = $121.

Therefore, the the rate is not constant, Option 2 is exponential.

Part B)

For Option 1)

Since it is a linear function, we can use the standard linear function given by:

`f(n)=mn+b`

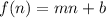
Where m is the slope and b is the y-intercept.

Since we started with $1000, our b is 1000.

And since the investment increases $100 for each year n, our slope m is 100. Therefore:

`f(n)=100n+1000`

For Option 2)

Since it is an exponential function, we can use the standard exponential function given by:

`f(n)=a(r)^n`

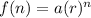
Where a is the initial value and r is the rate of growth.

We don't actually know the rate of growth, but we can find it. First, since the initial investment is $1000, substitute 1000 for a. This yields:

`f(n)=1000(r)^n`

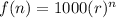
Since we know that the investment reached $1100 after one year, let's substitute 1100 for f(n) and 1 for n. This yields:

`1100=1000(r)^1`

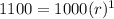
Divide both sides by 1000. Simplify:

`r=1.1`

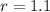
Therefore, our rate of growth is 1.1. So, our function is:.

`f(n)=1000(1.1)^n`

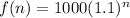
Part C)

To find the investment value after 20 years, we can use. our functions.

For Option 1)

Substitute 20 for n:

`f(20)=100(20)+1000`

Evaluate:

`f(20)=2000+1000=\$3000`

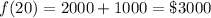
For Option 2)

Substitute 20 for n:

`f(20)=1000(1.1)^(20)`

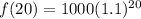
Evaluate:

`f(20)\approx\$6727.50`

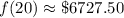
Therefore, if we used Option 2, we will earn an additional $6727 - $3000 = $3727. This is hugely significant, so Belinda should invest using Option 2.