Answer:
(a) 27°
(b) 17.9m
Explanation:
According to the attachment
⠀
let AB be the ladder
BC be the distance between the ladder and wall
⠀
(a) We have to find ∠A by trigonometry formula
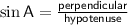
Here angle A is facing BC so it is perpendicular
and AB is the longest side so it is hypotenuse
(b)
AC is the distance from the upper end of the ladder to ground
we will find it by Pythagoras theorem
