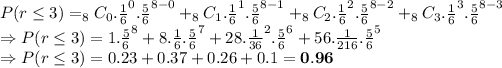Question

Suppose that you roll a die 8 times. What is the probability that you roll a six three or fewer times

Answer 1

0.96

Explanation:

Given that the a die is rolled 8 number of times.

`n` = 8

Probability of getting a 6 on roll of a die,
`p=(1)/(6)`

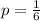
Probability of not getting a 6 on roll of a die,
`q=1-p=1-(1)/(6)=(5)/(6)`

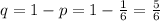
Probability of getting 6 three or fewer times:

`P(r \le 3)=P(r=0)+P(r=1)+P(r=2)+P(r=3)`

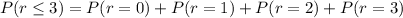
Formula:

`P(r=k)=_nC_k.p^k.q^(n-k)`

Putting the values using this formula:

`P(r \le 3)=_8C_0.(1)/(6)^0.(5)/(6)^(8-0)+_8C_1.(1)/(6)^1.(5)/(6)^(8-1)+_8C_2.(1)/(6)^2.(5)/(6)^(8-2)+_8C_3.(1)/(6)^3.(5)/(6)^(8-3)\\\Rightarrow P(r \le 3)=1.(5)/(6)^(8)+8.(1)/(6).(5)/(6)^(7)+28.(1)/(36)^2.(5)/(6)^(6)+56.(1)/(216).(5)/(6)^(5)\\\Rightarrow P(r \le 3)=0.23+0.37+0.26+0.1=\bold{0.96}`