Question

A tangent PQ at a point P of a circle of radius. 5cm meets a line through the centre O at a point Q so that OQ = 12 cm. Length PQ is :

A)12 cm

B) 13 cm

C) 8.5 cm

D) √119 cm​

Answer 1

`\boxed{D) √(119) \: cm}`

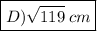
Solution :

In the above figure, the line that is drawn from the centre of the given circle to the targent PQ is perpendicular to PQ.

And So, OP ⊥ PQ

Using Pythagoras theorem in triangle ΔOPQ we get ,

`\Longrightarrow\: OQ^2 = OP^2 + PQ^2`

`\: \: \: \: \: \: \: \: \: \: \: \:`

`\Longrightarrow\: (12)^2 = 5^2+PQ^2`

`\: \: \: \: \: \: \: \: \: \: \: \:`

`\Longrightarrow\: PQ^2 = 144-25`

`\: \: \: \: \: \: \: \: \: \: \: \:`

`\Longrightarrow\: PQ^2 = 119`

`\: \: \: \: \: \: \: \: \: \: \: \:`

`\Longrightarrow\: PQ = √(119)`

`\: \: \: \: \: \: \: \: \: \: \: \:`

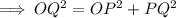
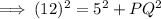
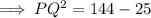
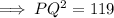
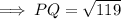
So, option D) √119 cm is the length of PQ.