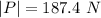Answer:
The value is
Step-by-step explanation:
From the question we are told that
The length of the first rope is L = 6 m
The first rope lie on the x-axis
The end point of the first rope is A
Now the vector of A will be
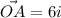
The point of the second rope on the wall is B
The coordinate for the point of the second rope on the wall is (0,-1,2)
The vector of B will be
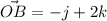
Now the coordinate of rope AB is mathematically represented as
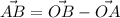
=>
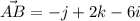
=>
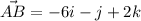
Generally the magnitude of the rope AB is mathematically evaluated as
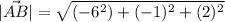
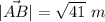
Generally the unit vector rope AB is mathematically evaluated as
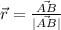
=>
![\vec r = (1)/(√(41) ) * [-6i -j+ 2k]](https://img.qammunity.org/2021/formulas/physics/college/3nmp6wp7gk5sjc4xefk4i3cntqtum09gbf.png)
From the question we are told that there is a force acting at point A and the force is
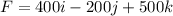
Generally the projected component of this force (in N) acting along the rope AB is mathematically represented as
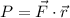
=>
![P = 400 i - 200 j + 500 k \ * \ (1)/(√(41) ) * [-6i -j+ 2k]](https://img.qammunity.org/2021/formulas/physics/college/615x65mymuqgma8hchxxbgfh8wmcc23r4i.png)
Note ( i . i = 1 ) , (j . j = 1) , (k . k = 1)
So
![P = (1)/(√(41) ) [-400 * 6 + 200 * 1 + 500 *2]](https://img.qammunity.org/2021/formulas/physics/college/hm0bcxufwthtuc72jfpzeadfxrshn1v6mf.png)
=>

So the magnitude of the projected component of this force (in N) acting along the rope AB is