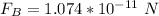Answer:
The value is
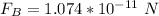
Step-by-step explanation:
From the question we are told that
The mass of the lithium nucleus is
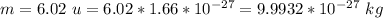
The radius is
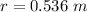
The speed of the lithium nucleus is
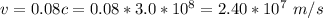
Given that the lithium nucleus is travelling in a circular path, the magnetic force will be equivalent to a centripetal force so
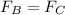
And
![F_C[tex] is centripetal force mathematically represented as </p><p> [tex]F_C = (m * v^2)/(r)](https://img.qammunity.org/2021/formulas/physics/college/o1qf92a4nmt3sno7rdpp07qpq3vj6te5mf.png)
So
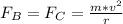
=>
![F_B = F_C = (9.9932*10^(-27) * [2.40*10^(7)]^2)/( 0.536)](https://img.qammunity.org/2021/formulas/physics/college/twwsdnszrssanrtjm2r32npf6drfvu9cbr.png)
=>