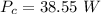Answer:
The value of the power is
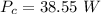
Step-by-step explanation:
From the question we are told that
The power rating
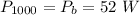
The frequency is
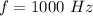
The frequency at which the sound intensity decreases
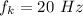
The decrease in intensity is by
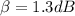
Generally the initial intensity of the speaker is mathematically represented as
![\beta_1 = 10 log_(10) [(P_b)/(P_a) ]](https://img.qammunity.org/2021/formulas/physics/college/tl9lbfmk2x0jobqj68ee6bd7cru3m95pou.png)
Generally the intensity of the speaker after it has been decreased is
![\beta_2 = 10 log_(10) [(P_c)/(P_a) ]](https://img.qammunity.org/2021/formulas/physics/college/wo77b09l0g567q1zkdh0fq5htn0uu5vo94.png)
So
![\beta_1-\beta_2 = 10 log_(10) [(P_c)/(P_a) ]- 10 log_(10) [(P_b)/(P_a) ]](https://img.qammunity.org/2021/formulas/physics/college/wgyh1hm3uknd1eehz42efa6jcs660in9sh.png)
=>
![\beta = 10 log_(10) [(P_c)/(P_a) ]- 10 log_(10) [(P_b)/(P_a) ]= 1.3](https://img.qammunity.org/2021/formulas/physics/college/1sfzloswelb6wd3p1benczoudbts3ewa8f.png)
=>
![\beta =10log_(10) [((P_b)/(P_a))/((P_c)/(P_a)) ] = 1.3](https://img.qammunity.org/2021/formulas/physics/college/43e33vdr52dkvtebnisrc7ibg6swzrcb90.png)
=>
![\beta =10log_(10) [(P_b)/(P_c) ] = 1.3](https://img.qammunity.org/2021/formulas/physics/college/2f7j4gmxjle1aybgp2l75269hzmnd7eoke.png)
=>
![10log_(10) [(P_b)/(P_c) ] = 1.3](https://img.qammunity.org/2021/formulas/physics/college/r9qf2sjwanzi3oaf2ninvr8t7hdbs2r6un.png)
=>
![log_(10) [(P_b)/(P_c) ] = 0.13](https://img.qammunity.org/2021/formulas/physics/college/3nlmvy2xww2vk3joigllekpmlt4kd9ktnb.png)
taking atilog of both sides
![[(P_b)/(P_c) ] = 10^(0.13)](https://img.qammunity.org/2021/formulas/physics/college/ijf3vwkuydgh8ppzckxb5afeh62ni3is5q.png)
=>
![[(52)/(P_c) ] = 10^(0.13)](https://img.qammunity.org/2021/formulas/physics/college/imsfqn23spdi8y5p151ielo80wd4fnmhsu.png)
=>
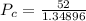
=>