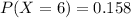Question

According to a survey, 74% of households said that they have never purchased organic fruits or vegetables. Suppose that this result is true for the current population of households. a. Let x be a binomial random variable that denotes the number of households in a random sample of 10 who have never purchased organic fruits or vegetables. What are the possible values that x can assume

Answer 1

Complete Question

According to a survey, 74% of households said that they have never purchased organic fruits or vegetables. Suppose that this result is true for the current population of households. a. Let x be a binomial random variable that denotes the number of households in a random sample of 10 who have never purchased organic fruits or vegetables. What are the possible values that x can assume? Integers to . b. Find to 3 decimal places the probability that exactly 6 households in a random sample of 10 will say that they have never purchased organic fruits or vegetables. Use the binomial probability distribution formula. Probability

Answer:

a

The possible value of x is 0, 1 ,2,3,4,5,6,7,8,9,10

b

`P(X = 6) =   0.158`

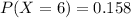
Explanation:

From the question we are told that

The proportion that stated that they have not purchased organic fruits or vegetables is
`p =0.74`

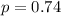
The sample size is n = 10

The possible value x can take is 0, 1 ,2,3,4,5,6,7,8,9,10

Generally the probability that exactly 6 households in a random sample of 10 will say that they have never purchased organic fruits or vegetables is mathematically represented as

`P(X = 6) =  ^nC_6 * p^(6)* (1-p)^(n-6)`

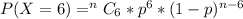
Here C denotes combination

So

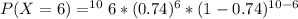
`P(X = 6) =  ^(10)6 * (0.74)^(6)* (1-0.74)^(10-6)`

=>
`P(X = 6) =   0.158`