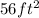Answer:
The largest area she can enclose for her garden with this fencing is
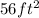
Explanation:
Suppose the rectangular space Mrs. Greene wants to plant has dimensions x feet and y feet.
Since each section of fencing is 1-foot long, both x and y must be integer numbers.
The perimeter of the rectangular space is calculated as:
P = 2x + 2y
And we know she uses all 30 sections of fencing, thus:
2x + 2y = 30, where x, y are integers and positive.
Simplifying by 2:
x + y = 15
Solve for x:
x = 15 - y
This equation doesn't have infinitely many solutions, since both numbers must be integers and positive. Suppose we start by setting y=1, then x=14. That is a possible arrangement for the garden.
Another valid option is for y=2, x=13
Continuing with these patterns, we find the maximum value for y is 7, x=8, because if we set y=8, x=7, this is the same condition as y=7, x=8.
Thus, from y=1 to y=7, there are 8 possible combinations for the arrangement of the garden.
The area of a rectangle is
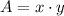
Testing some possible arrangements:
y=1, x=14
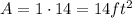
y=2, x=13

y=3, x=12
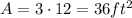
We can notice the combination y=7, x=8 has an area of:
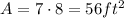
This is the largest possible area of all combinations, thus:
The largest area she can enclose for her garden with this fencing is