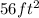Question

Mrs. Greene wants to plant a vegetable garden in her yard. She purchased a package containing 30 sections of fencing, each 1-foot long If she uses all 30 sections to create rectangular space, how many different arrangements are possible? What is the largest area she can enclose for her garden with this fencing?

Answer 1

The largest area she can enclose for her garden with this fencing is
`56 ft^2`

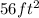
Explanation:

Suppose the rectangular space Mrs. Greene wants to plant has dimensions x feet and y feet.

Since each section of fencing is 1-foot long, both x and y must be integer numbers.

The perimeter of the rectangular space is calculated as:

P = 2x + 2y

And we know she uses all 30 sections of fencing, thus:

2x + 2y = 30, where x, y are integers and positive.

Simplifying by 2:

x + y = 15

Solve for x:

x = 15 - y

This equation doesn't have infinitely many solutions, since both numbers must be integers and positive. Suppose we start by setting y=1, then x=14. That is a possible arrangement for the garden.

Another valid option is for y=2, x=13

Continuing with these patterns, we find the maximum value for y is 7, x=8, because if we set y=8, x=7, this is the same condition as y=7, x=8.

Thus, from y=1 to y=7, there are 8 possible combinations for the arrangement of the garden.

The area of a rectangle is

`A=x\cdot y`

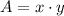
Testing some possible arrangements:

y=1, x=14

`A=1\cdot 14= 14 ft^2`

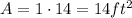
y=2, x=13

`A=2\cdot 13= 26 ft^2`

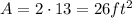
y=3, x=12

`A=3\cdot 12= 36 ft^2`

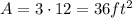
We can notice the combination y=7, x=8 has an area of:

`A=7\cdot 8= 56 ft^2`

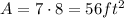
This is the largest possible area of all combinations, thus:

The largest area she can enclose for her garden with this fencing is
`56 ft^2`