Answer:
The Decision Rule
Fail to reject the null hypothesis
The conclusion
There is no sufficient evidence to support the claim that the mean age of the cars is greater than that of taxi
Explanation:
From the question we are told that
The data is
Car Ages 4 0 8 11 14 3 4 4 3 5 8 3 3 7 4 6 6 1 8 2 15 11 4 1 6 1 8
Taxi Ages 8 8 0 3 8 4 3 3 6 11 7 7 6 9 5 10 8 4 3 4
The level of significance
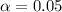
Generally the null hypothesis is
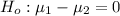
the alternative hypothesis is
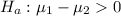
Generally the sample mean for the age of cars is mathematically represented as
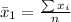
=>
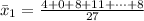
=>
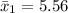
Generally the standard deviation of age of cars
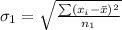
=>
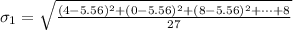
=>
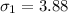
Generally the sample mean for the age of taxi is mathematically represented as
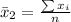
=>
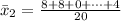
=>
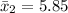
Generally the standard deviation of age of taxi
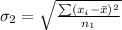
=>
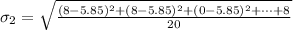
=>
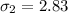
Generally the test statistics is mathematically represented as
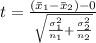
=>
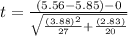
=>
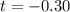
Generally the degree of freedom is mathematically represented as
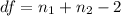
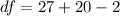
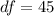
From the t distribution table the
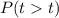 at the obtained degree of freedom = 45 is
at the obtained degree of freedom = 45 is
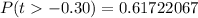
So the p-value is
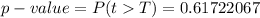
From the obtained values we see that the p-value >
 hence we fail to reject the null hypothesis
hence we fail to reject the null hypothesis
Hence the there is no sufficient evidence to support the claim that the mean age of the cars is greater than that of taxi