Question

Suppose that the function LaTeX: f(x) f ( x ) is shifted horizontally to the right by LaTeX: a a , reflected across the LaTeX: x x -axis, and shifted vertically down by LaTeX: b b to become the function LaTeX: g(x) g ( x ) . Write the function LaTeX: g(x) g ( x ) in terms of LaTeX: f(x) f ( x ) and explain each of the shifts

Answer 1

`g(x) = (x-a,-y - b)`

Explanation:

Given

Represent f(x) as follows:

`f(x) = (x,y)`

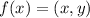
Transformations:

Horizontally shifted right by a

Reflected across x axis

Vertically shifted down by b

Taking the transformations one after the other.

Horizontally shifted right by a

When a function is shifted right, the resulting function is:

`f' = (x-a,y)`

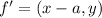
Reflected across x axis

Here, the x axis remains unaltered while the y axis is negated

`f' = (x-a,y)`

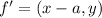
becomes

`f`

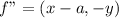
Vertically shifted down by b

When a function is shifted down by b, the resulting function is:

`f`

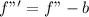
i.e, subtract b from the function (f(x) or y, as the case may be)

So, we have:

`f`

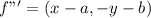
Represent f"' with g(x)

`g(x) = (x-a,-y - b)`