Answer:
The area of the triangle is 12 unit²
Explanation:
The vertices of the triangle are;
a(2, 5), b(5, 9), and c(8, 5)
The area of a triangle given coordinates can be given by the following determinant;
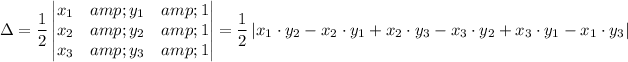
Therefore, we have;
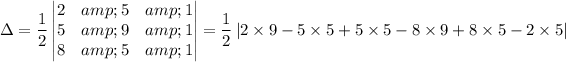
Utilizing an online determinant calculator, we have;
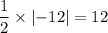
Therefore, the area of the triangle is 12 unit².