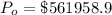Question

A 2000-gallon metal tank to store hazardous materials was bought 15 years ago at cost of $100,000. What will a 5,000-gallon tank cost today if the power–sizing exponent is 0.57 and the construction cost index for such facilities has increased from 180 to 600 over the last 15 years? Choose the closest value.

Answer 1

The value is
`P_o = \$ 561958.9`

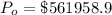
Explanation:

From the question we are told that

The capacity of the metal tank is
`C =  2000 \  gallon`

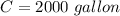
The duration usage is
`t = 15\ years \ ago`

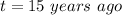
The cost of 2000-gallon tank 15 years ago is
`P =  \$100,000`

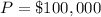
The capacity of the second tank considered is
`C_1 = 5,000`

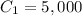
The power sizing exponent is
`e = 0.57`

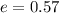
The initial construction cost index is
`u_1 = 180`

The new construction after 15 years cost index is
`u_2 =600`

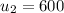
Equation for the power sizing exponent is mathematically represented as

`(P_n)/(P) = [(C_1)/(C) ]^(e)`

=> Here
`P_n` is the cost of 5,000-gallon tank as at 15 years ago

So

`P_n  =  [(5000)/(2000) ] ^(0.57) * 100000`

`P_n  =  \$168587.7`

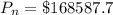
Equation for the cost index exponent is mathematically represented as

`(P_o)/(P_n)  =  (u_2)/(u_1)`

Here
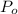`P_o` is the cost of 5,000-gallon tank today

So

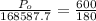
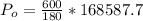
`(P_o)/(168587.7)  =  (600)/(180)`

=>
`P_o = (600)/(180) * 168587.7`

=>
`P_o = \$ 561958.9`