Given:
Area of rectangle =
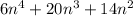
Width of the rectangle is equal to the greatest common monomial factor of
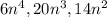 .
.
To find:
Length and width of the rectangle.
Solution:
Width of the rectangle is equal to the greatest common monomial factor of
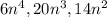 is
is

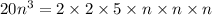

Now,
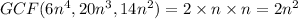
So, width of the rectangle is
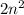 .
.
Area of rectangle is
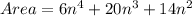
Taking out GCF, we get

We know that, area of a rectangle is the product of its length and width.
Since, width of the rectangle is
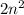 , therefore length of the rectangle is
, therefore length of the rectangle is
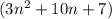 .
.