Answer:
Maddie is correct.
Explanation:
Give that Molly has $100.00 and a coupon for a $10.00 discount.
The cost of 1 shirt = $ 15.00
Let Molly can buy a maximum of x t-shirt.
Note that must be a counting number ( integer) as the number of t-shirts can't be a fractional number.
So, the cost of x t-shirts = $ 15x
As she has a discount coupon, so the cost she has to pay after using the discount coupon is $15x-$10, which must not be greater than the money she has, i.e $100.
So, the required inequality is
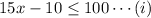
As given, Molly's equation is 15x + 10 = 100 and Maddie's equation is 15x - 10 = 100.
Maddie's equation is partially correct in comparison with the equation (i) as there is a sign of equality only.
Now, solving the equation (i), we have
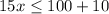
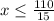
 .
.
As x must be an integer, so the possible value of x is 7.
Hence, she can buy a maximum of t-shirts, so, Maddie is correct.