Question

Which are correct representations of the inequality –3(2x – 5) < 5(2 – x)? Select two options. x < 5 –6x – 5 < 10 – x –6x + 15 < 10 – 5x A number line from negative 3 to 3 in increments of 1. An open circle is at 5 and a bold line starts at 5 and is pointing to the right. A number line from negative 3 to 3 in increments of 1. An open circle is at negative 5 and a bold line starts at negative 5 and is pointing to the left.

Answer 1

C.)–6x + 15 < 10 – 5x

D.)A number line from negative 3 to 3 in increments of 1. An open circle is at 5 and a bold line starts at 5 and is pointing to the right.

Hope this helps and have a nice day :)

Explanation:

Answer 2

Given:

The inequality is

`-3(2x-5)<5(2-x)`

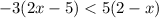
To find:

The correct representations of the given inequality.

Solution:

We have,

`-3(2x-5)<5(2-x)`

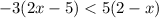
Using distributive property, we get

`-3(2x)-3(-5)<5(2)+5(-x)`

`-6x+15<10-5x`

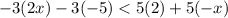
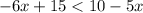
Therefore, the correct option is C.

Isolate variable terms.

`15-10<6x-5x`

`5<x`

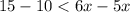
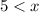
It means, the value of x is greater than 5.

Since 5 is not included in the solution set, therefore, there is an open circle at 5.

So, the graphical represents of the solution is a A number line from negative 3 to 3 in increments of 1. An open circle is at 5 and a bold line starts at 5 and is pointing to the right.

Therefore, the correct option is D.