Question

Dos pilotos suicidas, que están inicialmente a una distancia de 500 m entre sí, deciden chocar directamente de frente arrancando ambos desde el reposo. Ambos autos pueden desarrollar una aceleración máxima constante de 15 m/s2 . Si el piloto A arranca un segundo antes que el piloto B, encuentra: a) la posición donde los autos chocan, medida a partir de la posición donde arranca el piloto A, y b) la rapidez relativa de la colisión (la rapidez de B con respecto a A justo antes de la colisión, ó viceversa).

Answer 1

a) El punto de colisión de los dos automóviles desde donde parte el conductor del automóvil A es de aproximadamente 293,14 metros.

b) La velocidad del automóvil A, en relación con la velocidad del automóvil B, es de 15 m / s

Step-by-step explanation:

Los parámetros del movimiento son;

La distancia entre ambos coches = 500 m

La aceleración de ambos coches = 15 m / s²

La dirección de movimiento de ambos coches = uno hacia el otro

La hora de inicio del conductor A = Un segundo antes de la hora de inicio del conductor B

Por lo tanto, de la ecuación de movimiento, tenemos;

s = u · t + 1/2 · a · t²

v² = u² + 2 · a · s

Dónde;

u = La velocidad inicial de los autos = 0 (los autos parten del reposo)

t = El tiempo de movimiento de una aceleración dada

a = La aceleración = 15 m / s²

s = La distancia recorrida en el tiempo t

Por lo tanto, para el controlador A, tenemos;

s₁ = 0 × (t + 1) + 1/2 × 15 × (t + 1) ² = 7.5 × (t + 1) ²

s₁ = 7.5 × (t + 1) ²

Para el conductor B, tenemos;

s₂ = 0 × t + 1/2 × 15 × t² = 7.5 × t²

s₂ = 7,5 × t²

Dado que ambos chocan a lo largo del camino de 500 m, tenemos;

s₁ + s₂ = 500 metros

∴ 7.5 × (t + 1) ² + 7.5 × t² = 500

∵ s₁ + s₂ = 7.5 × (t + 1) ² + 7.5 × t²

Lo que da;

15 · t² + 15 · t + 7.5 = 500

15 · t² + 15 · t - 492,5 = 0

Resolver usando la aplicación en línea da; t = -6,25181 o t = 5,25181

Dado que t es un número natural, tenemos el valor correcto para t = 5.25181 segundos

a) Por tanto, el punto de colisión de los dos coches desde donde parte el conductor del coche A es;

s₁ = 7.5 × (t + 1) ² = 7.5 × (5.25181 + 1) ² ≈ 293.14 metros

El punto de colisión de los dos automóviles desde donde parte el conductor del automóvil A ≈ 293,14 metros

b) La semilla de A en el punto de colisión se da de la siguiente manera

Velocidad, v₁ = u + a × (t + 1) = 0 + 15 × (5.25181 + 1) ≈ 93.78

v₁ ≈ 93,78 m / s

La semilla de B en el punto de colisión también se da de la siguiente manera

Velocidad, v = u + a × (t) = 0 + 15 × 5.25181 ≈ 78.78

v₁ ≈ 78,78 m / s

Por lo tanto, la velocidad del automóvil A, en relación con la velocidad del automóvil B,
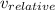`v_(relative)` se da como sigue;

= v₁ - v₂ = 93,78 m / s - 78,78 m / s = 15 m / s

la velocidad del automóvil A, relativa a la velocidad del automóvil B = 15 m/s.