Question

The changes in housing prices over short time periods are in part determined by supply and demand. A real estate company in Minnesota projected an increase in its average selling prices of homes in the first quarter of 2014 over the mean 2013 selling price of $201,800. The reason for the projection was an increase in demand due to business expansion and the subsequent increase in labor. To investigate the accuracy of the projection, a sample of homes in the first quarter of 2014 was selected and the following selling prices (in $) recorded:

235,000 271,900 183,300 203,000 182,900 225,500 189,000 214,200 237,900 233,500 217,000 230,400 202,950, 216,500 209,900, 245,500

Required:
a. At 5% level of significance, is there sufficient evidence to support the real estate company's projection?
b. Which statistical distribution should be applied in this situation and why? Explain carefully.
c. Discuss the consequences of Type I and Type II errors in terms of the problem.
d. Does the management at the real estate company want a small or large value of the significance level? Explain carefully.
e. Based on a 95% confidence level, estimate the actual average selling price homes in the first quarter of 2014.

Answer 1

The data given is

235,000 271,900 183,300 203,000 182,900 225,500 189,000 214,200 237,900 233,500 217,000 230,400 202,950, 216,500 209,900, 245,500

The sample size is n = 16

The population is
`\mu  =  \$201,800`

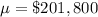
The sample mean is mathematically represented as

`\= x =(\sum x_i)/(n)`

=>
`\= x  =(235,000 + 271,900 + \cdots + 245,500 )/(16)`

=>
`\= x  = 218653.125`

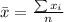
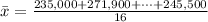
Generally the sample standard deviation is mathematically represented as

`s =  \sqrt{(\sum (x_i - \= x)^2)/(n) }`

=>
`s =  \sqrt{( (235,000 -  218653.125)^2+ (271,900 -  218653.125)^2 + \cdots +  (245,500 -  218653.125)^2)/(16) }`

=>
`s =  23946.896`

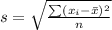
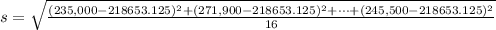
The null hypothesis is
`H_o : \mu =  \$201,800`

The alternatively hypothesis is
`H_o : \mu >  \$201,800`

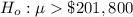
Generally the test statistics is mathematically represented as

`t =  (\= x  - \mu )/( (s)/(√(n) ) )`

=>
`t =  (218653.125  - 201800 )/( (23946.896 )/(√(16) ) )`

=>
`t =  2.82`

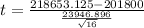
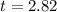
Generally the degree of freedom is mathematically represented as

`df =  n - 1`

=>
`df =  16 - 1`

=>
`df =  15`

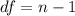
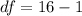
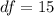
Generally the probability of
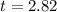`t =  2.82` at a degree of freedom of
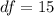`df =  15` from the t - distribution table is

`p-value  = P( t >2.82 ) =0.00646356`

The

From the values obtained we see that
`p-value  < \alpha`

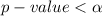
The decision rule is

Reject the null hypothesis

The conclusion is

There is sufficient evidence to conclude that the real estate company's projection is true

Given that the population variance is unknown then the best statistical distribution to be applied is the t -distribution

Type I Error

The type 1 error occur when the null hypothesis is wrongfully rejected

The consequence in this case is the company will assume that the average selling price has increase and this will lead the company to start expanding the business while in the real sense the average selling price is still $201,800

Type II Error

The type 11 error occur when the null hypothesis is wrongfully accepted(i.e wrongfully failed to reject the null hypothesis)

The consequence in this case is that the company will assume that the average selling price is still $201,800 and will not make plans to increase the business while in the real sense the average selling price has increased

Given that resource is scare the management of the company will want a smaller significance level in order not to commit type I error which will lead to wrongly expanding the business and wastes of resources

generally the critical value of
`(\alpha )/(2)` from the normal distribution table is

`Z_{(\alpha )/(2) } = 1.96`

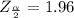
Generally the margin of error is mathematically represented as

`E  =Z_{(\alpha )/(2) } *  (s)/(√(n) )`

=>
`E  =1.96*  (23946.896)/(√(16) )`

=>
`E  = 11733.96`

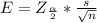
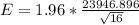
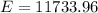
Generally the 95% confidence interval is mathematically represented as

`218653.125 - 11733.96  < \mu  <  218653.125 + 11733.96`

=>
`206919.165  < \mu  <  230387.085`

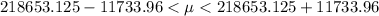
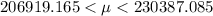
Generally there is 95% confidence that the actual average selling price is within this interval

Explanation: