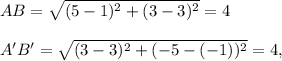Question

Line segment AB is shown on a coordinate grid: A coordinate grid is shown from positive 6 to negative 6 on the x-axis and from positive 6 to negative 6 on the y-axis. A line segment AB is shown with A as ordered pair 1, 3 and B as ordered pair 5, 3. The line segment is rotated 270 degrees counterclockwise about the origin to form A′B′. Which statement describes A′B′? (5 points) A′B′ is parallel to AB. A′B′ is half the length of AB. A′B′ and AB are equal in length. A′B′ is greater than twice the length of AB.

Answer 1

A′B′ and AB are equal in length.

Explanation:

Given that the location of the points are at A(1, 3) and B(5, 3).

Transformation is the movement of a point from its initial location to a new location. Types of transformation are reflection, rotation, translation and dilation.

Rigid transformation are transformation that preserves the shape and size when performed. Types of rigid transformation are reflection, rotation, translation.

Hence if AB is rotated 270 degrees counterclockwise about the origin to form A′B′, both A′B′ and AB are equal in length because rotation is a rigid transformation.

If A(x,y) is rotated 270 degrees counterclockwise about the origin, it becomes A'(y,-x).

Hence if AB is rotated 270 degrees counterclockwise about the origin to form A'(3, -1), B'(3, -5)

`AB=√((5-1)^2+(3-3)^2) =4\\\\A'B'=√((3-3)^2+(-5-(-1))^2)=4,`