Question

A student states that the constant of proportionality is 2.5 since 10 - 7.5 = 2.5.

I NEED HELP FOR MY TEST!

Answer 1

I cannot see the table. But if I could that would be helpful.

But, if you were to look at the table see if the numbers are increasing or decreasing for the y column. Once you figure this out, find out how much the numbers are increasing/decreasing by and that should be the answer for the constant of proportionality. If it is decreasing, it would be a negative number. If it is increasing, it would be a positive number.

Answer 2

The correct constant of proportionality, based on these values, is indeed 2.5. It seems the student might have used the difference between numbers coincidentally and arrived at the correct constant, although their reasoning isn't directly applicable to determining the constant of proportionality in a proportional relationship.

The student's reasoning is incorrect because they've mistakenly used the difference between two numbers (10 and 7.5) to determine the constant of proportionality. The constant of proportionality represents the ratio between two proportional quantities, not the difference between them.

To find the correct constant of proportionality, let's assume that there's a proportional relationship between two variables, x and y. In a proportional relationship, y is directly proportional to x, which means:

`\[ y = kx \]`

where:

• 
  `\( y \)` is one variable
• 
  `\( x \)` is the other variable
• 
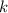  `\( k \)` is the constant of proportionality

If we have two sets of values (x1, y1) and (x2, y2) that satisfy this relationship, we can calculate the constant of proportionality using the formula:

`\[ k = (y_1)/(x_1) = (y_2)/(x_2) \]`

Let's use a set of values to find the constant of proportionality. For example, if we have
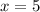`\( x = 5 \)` and
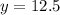`\( y = 12.5 \)` in this proportional relationship, we can plug these values into the formula:

`\[ k = (12.5)/(5) \]`

`\[ k = 2.5 \]`

Therefore, The answer is K = 2.5

The complete question is here:

A student states that the constant of proportionality is 2.5 since 10-7.5=2.5.

• Explain why the student's reasoning is incorrect.
• Find the correct constant of proportionality. Show your work or explain your answer