Answer:
56.5 ft
Explanation:
See the attached figure which represents the explanation of the problem.
We need to find the length of the tree to which is the length of AD
From the graph ∠BAC = 90° and ∠ABD = 76°, AB = 18 ft
At ΔABD:
∠BAD = ∠BAC - ∠DAC = 90° - 4° = 86°
∠ADB = 180° - ( ∠BAD + ∠ABD) = 180 - (86+76) = 180 - 162 = 18°
Apply the sine rule at ΔABD
∴
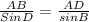
∴ 18/sin 18 = AD/sin 76
∴ AD = 18 * (sin 76)/(sin 18) ≈ 56.5 (to the nearest tenth of a foot)
So, The length of the tree = 56.5 ft.
The answer is 56.5 ft