Question

F(n)=2n+1
g(n)=3n
Find f(n)+g(n)

Answer 1

`\boxed {\tt f(n)+g(n)=5n+1}`

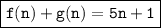
Explanation:

We want to find f(n) + g(n) . Basically, we have to find the sum of f(n) and g(n).

`f(n)+g(n)`

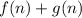
We know that:

`f(n)=2n+1\\g(n)=3n`

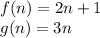
Therefore, we can substitute 2n+1 in for f(n) and 3n in for g(n)

`(2n+1)+(3n)`

Combine like terms. The terms 3n and 2n both have a "n" so they can be combined.

`(2n+3n)+(1)`

`(5n)+1`

`5n+1`

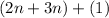
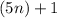
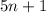
f(n)+g(n) is equal to 5n+1

Answer 2

`\longrightarrow 5n+1\longleftarrow`

Explanation:

`f(n)=2n+1\\\\g(n)=3n\\\\f(n)+g(n)=?\\\\\longrightarrow (2n+1)\longleftarrow\\\\+\longrightarrow (3n)\longleftarrow\\\\f(n)+g(n)=2n+1+3n\\\\=(2n+3n)+1\\\\=(2+3)n+1\\\\=5n+1\longleftarrow \\\\\dagger`