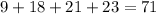Question

The sum of four siblings ages is 71. The second child’s age is twice the youngest, the third child’s age is twelve more than the youngest, and the oldest child is four less than three times the youngest. Find each of the siblings ages.

Answer 1

Answer: 9, 18, 21, and 23 respectively

Explanation:

To solve any problem like this, you want to assign a variable to each child because you dont know their age. So lets write an equation and assign variables to these children.

r = first child (youngest)

x = second child

y = third child

z = fourth child (oldest)

We know that r + x + y + z = 71

We also are given info on the comparisons of their ages.

r = r

x = 2r (2 times the youngest)

y = 12 + r (12 more than the youngest)

z = 3r - 4 (4 less than 3 times the youngest)

That was the easy part tbh, now we have to solve for 'r'. We can see that all the ages are a function of the same variable (r), and we know the sum of them is equal to 71. So lets solve for r and then plug that r value into each equation we just derived.

Child #1 (youngest)

`r+2r+(12+r)+(3r-4)=71\\3r+12+r+3r-4=71\\7r+12-4=71\\7r+8=71\\7r=63\\r=9yrs`

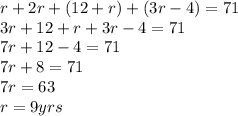
Child #2

`x=2*9=18yrs`

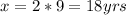
Child #3

`y=12+r=12+9=21yrs`

Child #4 (oldest)

`z=3r-4=(3*9)-4=27-4=23yrs`

Fact Check:

`9+18+21+23=71`