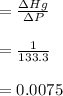Answer:
The answer "K = 0.0075"
Step-by-step explanation:
If we try to measure up to 69 kPa of air, find mercury or fluid for gauge.
While mercury was its largest liquid with a density of 13600 kg / m3 at normal room temperature.
Let's all measure for 69 kPa that height of the mercury liquid column.
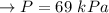
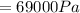
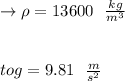
Formula:
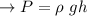

The right choice for pressure measurements up to 69 kPa is mercury.
Atmospheric Mercury up to 69 kPa Air 517 mm
The relationship of Hg to Pa is = 134.22 Pa 1 mm Hg
Static sensitivity to Pa of mm hg = change of mercury height to Pa: