Answer:
x ≥ 11 or x ≤ -3
Step-by-step explanation:
Hi there! Please take a look at the following explanation and let me know in comment if you have any questions!
Given:
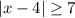
To solve an absolute inequality, consider the following theorems.
Theorems:
For b ≥ 0:
(1) If |x-a| ≥ b then we have x-a ≥ b or x-a ≤ -b so that we end up with x ≥ b+a, x ≤ -b+a
(2) If |x-a| ≤ b then we have -b ≤ x-a ≤ b which can be simplified to -b+a ≤ x ≤ b+a
Step:
From the inequality, we use the (1) theorem.

Therefore, the answer is x ≥ 11 or x ≤ -3