Question

A regional automobile dealership sent out fliers to prospective customers indicating that they had already won one of three different​ prizes: an automobile valued at ​$​, a ​$ gas​ card, or a ​$ shopping card. To claim his or her​ prize, a prospective customer needed to present the flier at the​ dealership's showroom. The fine print on the back of the flier listed the probabilities of winning. The chance of winning the car was 1 out of ​, the chance of winning the gas card was 1 out of and the chance of winning the shopping card was out of 31,866​, the chance of winning the gas card was 1 out of 31,866, and the chance of winning the shopping card was 31,864 out of 31,866.

Required:
a. How many fliers do you think the automobile dealership sent​ out?
b. Using your answer to​ (a) and the probabilities listed on the​ flier, what is the expected value of the prize won by a prospective customer receiving a​ flier?
c. Using your answer to​ (a) and the probabilities listed on the​ flier, what is the standard deviation of the value of the prize won by a prospective customer receiving a​ flier?

Answer 1

(a) 31101

(b) $5.65

(c) $113.38

Explanation:

The complete question is:

A regional automobile dealership sent out fliers to prospective customers indicating that they had already won one of three different prizes: an automobile valued at $20,000, a $125 gas card, or a $5 shopping card. To claim his or her prize, a prospective print on the back of the flier listed the probabilities of winning. The chance of winning the car was 1 out of 31,101, the chance of winning the gas card was 1 out of 31,101, and the chance of winning the shopping card was 31, 099 out of 31,101.

Solution:

The information provided is as follows:

`P(\text{Car})=(1)/(31101)\\\\P(\text{Gas Card})=(1)/(31101)\\\\P(\text{Shopping Card})=(31099)/(31101)`

(a)

The number of fliers the automobile dealership sent​ out is, n = 31,101.

This is because the probability of winning any of the three prize is out of 31,101.

(b)

Compute the expected value of the prize won by a prospective customer receiving a​ flier as follows:

`E(X)=\sum x* P(X=x)`

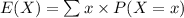
`=[20000* (1)/(31101)]+[125* (1)/(31101)]+[5* (31099)/(31101)]\\\\=0.6431+0.0040+4.9997\\\\=5.6468\\\\\approx 5.65`

Thus, the expected value of the prize won by a prospective customer receiving a​ flier is $5.65.

(c)

Compute the standard deviation of the prize won by a prospective customer receiving a​ flier as follows:

`SD(X)=√(V(X))=\sqrt{E(X^(2)-(E(X))^(2)}`

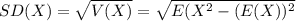
`=\sqrt{[(20000)^(2)* (1)/(31101)+(125)^(2)* (1)/(31101)+(5)^(2)* (31099)/(31101)]-(5.65)^(2)}\\\\=√(12854.9011)\\\\=113.37947\\\\\approx 113.38`

Thus, the standard deviation of the prize won by a prospective customer receiving a​ flier is $113.38.