Question

B^2 + 35 = −12b Solve each equation by factoring

I really need help with understanding this step by step, thank you. I am giving 40 points for this.

Answer 1

`b=-5, -7`

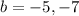
Explanation:

We have the equation
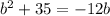`b^2+35=-12b` and we want to solve it by factoring.

First, let's move all the stuff to one side so that the other side is 0. So, let's add
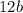`12b` to both sides. This yields:

`b^2+12b+35=0`

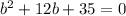
Let's review how to factor. If we have an equation in the following form:

`ax^2+bx+c=0`

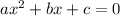
Where a, b, and c are the coefficients of the variable (in our example, our variable is b), then we must find two numbers, p and q, such that:

`pq=ac \text{ (p times q equals a times c) and}\\p+q=b \text{ (p plus q equals b)}`

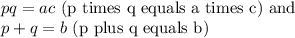
Our equation can be rewritten as:

`(1)b^2+(12)b+(35)=0`

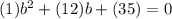
So, our a is 1, b is 12, and c is 35.

Therefore, we need to find two numbers that when multiplied together yields a(c) = 1(35) = 35 and we added together yields b = 12.

From here, we just have to guess and check. We can start by listing all the factors of 35. There aren't in fact that many:

`35: 1\text{ and } 35, 5\text{ and } 7`

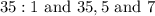
1 + 35 is 36, not 12. However, 5 + 7 is indeed 12. So, our two numbers p and q are 5 and 7.

Now what we've found our two numbers, we substitute the b term for our two numbers. We have:

`b^2+12b+35=0`

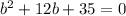
We will substitute 12b for 5b + 7b:

`b^2+5b+7b+35=0`

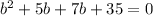
From here, we factor by grouping. From the first two terms, factor out a b:

`b(b+5)+7b+35=0`

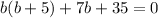
And from the last two terms, factor out a 7:

`b(b+5)+7(b+5)=0`

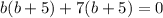
Now, notice that both terms have a
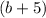`(b+5)`. So, by using grouping or the reverse of the distribute property, we can write:

`(b+7)(b+5)=0`

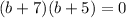
Notice that if we distribute the left term into the right, we get
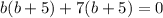`b(b+5)+7(b+5)=0`, so our equation is indeed equivalent.

So now we. have:

`(b+7)(b+5)=0`

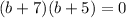
We can now use the Zero Product Property to acquire:

`b+7=0\text{ or } b+5=0`

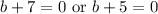
Solve for b for each case. Therefore, the solutions of our equation are:

`b=-7\text{ or } b=-5`

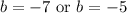
Notes:

If we can't find two numbers p and q that satisfy our conditions, this means that the equation cannot be factored. So, we will use alternative methods to solve our equation.