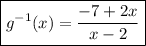Question

Find the inverse of the function. Show work.
g(x)= - 3/x-2 +2

Answer 1

`\displaystyle g^(-1)(x)=(-7+2x)/(x-2)`

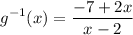
Explanation:

We are given the function:

`\displaystyle g(x)=-(3)/(x-2)+2`

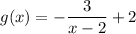
Let's find the inverse of g.

Call y=g(x):

`\displaystyle y=-(3)/(x-2)+2`

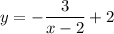
We need to solve for x. Multiply both sides by x-2 to eliminate denominators:

`y(x-2)=-3+2(x-2)`

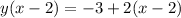
Operate:

`yx-2y=-3+2x-4`

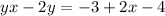
Collect the x's to the left side and the rest to the right side of the equation:

`yx-2x=-3-4+2y`

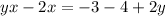
Factor the left side and operate on the right side:

`x(y-2)=-7+2y`

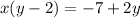
Solve for x:

`\displaystyle x=(-7+2y)/(y-2)`

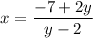
Interchange variables:

`\displaystyle y=(-7+2x)/(x-2)`

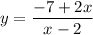
Call y as the inverse function:

`\boxed{\displaystyle g^(-1)(x)=(-7+2x)/(x-2)}`