
Find the equation of the line passing through (4, 5) and parallel to
3x-2y=4.

First of all, We need to convert this equation from standard form (ax+by=c) into slope-intercept form (y=mx+b).
 First, add 2y on both sides:-
First, add 2y on both sides:-
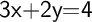
 Now, subtract 3x on both sides:-
Now, subtract 3x on both sides:-
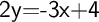
 Divide by 2 on both sides
Divide by 2 on both sides
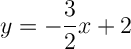

Now, let's find the equation of the line that's parallel to the given line.
Remember, if lines are parallel to each other, then their slope's the same.
So the slope of the line that's parallel to the line whose equation we just found, is
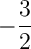
Now let's write the equation in point-slope form:-
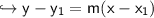
Replace numbers with letters, as follows:-
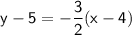
The equation above is the equation in point-slope form.
Incase you need it converted to slope intercept form, refer to the steps below ~
Multiply -3/2 times x and -4:-
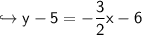
Now, Add 5 on both sides:-
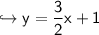
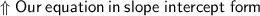
Good luck with your studies.
#TogetherWeGoFar
