Answer:
Step-by-step explanation:
From the information given:
a.
Using the equipartition theorem, the average energy of a molecule dor each degree of freedom is:
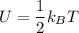
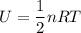
For s degree of freedom
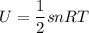
However, the molar specific heat
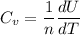
Therefore, in terms of R and s;
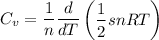
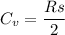
b.
Given that:
Cv=70.6Jmol⋅K and R=8.314Jmol⋅K
Then; using the formula
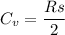
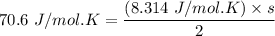

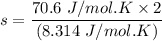
s = 16.983
s
 17
17