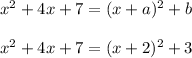Question

I RLLY NEED HELP PLS!!

Write each trinomial in the form (x+a)^2+b where a and b can be positive or negative.
x^2+4x+7

Answer 1

Answer:
`(x+2)^2+3\\\\`

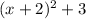
a = 2 and b = 3

==================================================

Step-by-step explanation:

Let's expand out
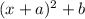`(x+a)^2+b` to get the following:

`(x+a)^2+b\\\\(x+a)(x+a)+b\\\\x(x+a)+a(x+a)+b\\\\x^2+ax+ax+a^2+b\\\\x^2+2ax+a^2+b\\\\`

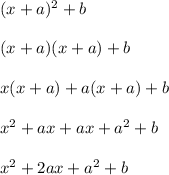
The x term here is 2ax

Compare this to the x term of
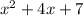`x^2+4x+7` and we see that

`2ax = 4x\\\\2a = 4\\\\a = 4/2\\\\a = 2\\\\`

--------------

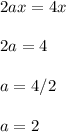
The constant term of
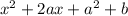`x^2+2ax+a^2+b\\\\` is the
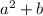`a^2+b` portion since it doesn't have the variable x attached to it.

Compare this with the 7 of
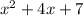`x^2+4x+7` which is also the constant.

Equate the two items, plug in a = 2 and solve for b.

`a^2+b = 7\\\\2^2+b = 7\\\\4+b = 7\\\\b = 7-4\\\\b = 3\\\\`

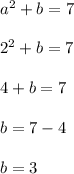
Therefore,

`x^2+4x+7 = (x+a)^2+b\\\\x^2+4x+7 = (x+2)^2+3\\\\`