
Solve the inequality for u:-
22≤-4u-2.

First, let's add 2 on both sides:-
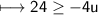
Switching the order (and flipping the inequality sign):-
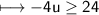
Divide by -4 on both sides:-
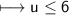
 Notice that the inequality sign changed from "less than" to "greater than". This happened because we divided by a negative number on both sides.
Notice that the inequality sign changed from "less than" to "greater than". This happened because we divided by a negative number on both sides.
- Henceforth, We conclude that:-

Good luck with your studies.
#TogetherWeGoFar
