Question

If it is known that 14y²-20y+48+√14y²-20y-15=9 then find the value of 14y²-20y+48-√14y²-20y-15=...

help me, pls :D!!!!!​

Answer 1

Answer: 7

==========================================================

Step-by-step explanation:

Let,

`A = √(14y^2 - 20y + 48)\\\\B = √(14y^2 - 20y - 15)\\\\`

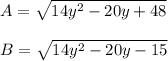
The first equation

`√(14y^2 - 20y + 48) + √(14y^2 - 20y - 15) = 9`

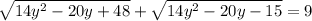
is in the form of

`A+B = 9`

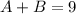
The goal is to find the value of

`√(14y^2 - 20y + 48) - √(14y^2 - 20y -15)`

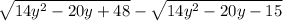
which is of the form
`A - B`

----------------

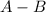
Use the difference of squares rule to say the following:

`(A+B)(A-B) = A^2 - B^2\\\\(A+B)(A-B) = \left(√(14y^2 - 20y + 48)\right)^2 -\left(√(14y^2 - 20y - 15 )\right)^2\\\\(A+B)(A-B) = (14y^2 - 20y + 48) -(14y^2 - 20y - 15 )\\\\(A+B)(A-B) = 14y^2 - 20y + 48 -14y^2 + 20y + 15 \\\\(A+B)(A-B) = (14y^2 -14y^2) +(- 20y + 20y) + (48+15) \\\\(A+B)(A-B) = 63 \\\\`

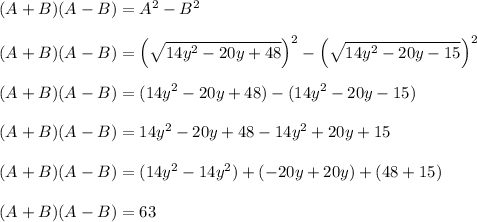
All of the y^2 and y terms cancel, leaving nothing but a single number.

The last thing to do is replace the A+B with 9, since A+B = 9 was mentioned earlier, and isolate A-B

Divide both sides by 9 to isolate A-B

`(A+B)(A-B) = 63 \\\\9(A-B) = 63 \\\\A-B = 63/9 \\\\A-B = 7 \\\\√(14y^2 - 20y + 48) - √(14y^2 - 20y - 15) = 7 \\\\`

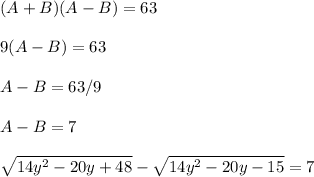
Therefore, 7 is the final answer.

----------------

An alternative is to solve the first equation for y.

It's messy but doable. I'll skip steps, but you should get y = -4/7 and y = 2 as the two solutions.

If you plugged y = -4/7 into the second expression, then you should end up with 7. The same goes for plugging in y = 2. Only pick one of those values.