Answer:
Area = 551 cm² (nearest whole number)
Explanation:
Circumference
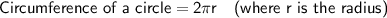
Given:
- Circumference = 83.21 cm
- π = 3.14
Substituting the given values into the formula and solving for r:

Area
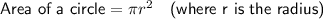
Given:
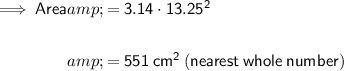
If the circumference of the hub cap was smaller, the radius would be smaller, hence the area would be smaller.