Question

The value of k for which the system of equations 2x + 3y = 5 and 4x + ky = 10 has infinite many

solution is

Answer 1

k = 6

Explanation:

Hi there! Please take a look at the following explanation and let me know in the comment if you have any doubts!

Given:

`\displaystyle \large{\begin{cases} 2x+3y=5 \\ 4x+ky=10 \end{cases}}`

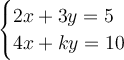
Problem:

We want to know the value of k that makes the simultaneous equation have infinitely many solutions.

Step:

To make simultaneous equation have infinitely many solutions, we can do by using graph visual method. The method says that if both graphs overlap one another then both equations have same slope and y-intercept. In other word, both equations must be the same to have infinitely many solutions.

From the simultaneous equation, if you notice we can simply multiply the first equation by 2 to make it look the same as the second equation.

`\displaystyle \large{\begin{cases} 2x\cdot 2 + 3y\cdot 2=5\cdot 2 \\ 4x+ky=10 \end{cases}}\\\\\displaystyle \large{\begin{cases} 4x+6y=10 \\ 4x+ky=10 \end{cases}}`

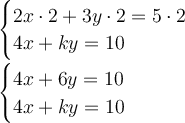
Compare the coefficient with both equations.

• 4x = 4x
• 6y = ky
• 10 = 10

Therefore, the value of k has to be 6.

Alternative Method:

Instead of multiply by 2 to the first equation, you can also multiply the second equation by 1/2 to get the similar equation like the first equation.

`\displaystyle \large{\begin{cases} 2x+3y=5 \\ 4x\cdot (1)/(2)+ky\cdot (1)/(2)=10 \cdot (1)/(2) \end{cases}}\\\\\displaystyle \large{\begin{cases} 2x+3y=5 \\ 2x+(k)/(2)y=5 \end{cases}}`

Compare the variables & coefficients.

• 2x = 2x
• 3 = k/2 —> 6 = k
• 5 = 5

Therefore, the value of k is still 6.

Alternative Method (2):

First, arrange the simultaneous equation in slope-intercept form which is y = mx + b

`\displaystyle \large{\begin{cases} y = -(2)/(3)x + (5)/(3) \\ y = -(4)/(k)x+\frac{10}k \end{cases}}`

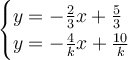
Since to make the simultaneous equation having infinitely many solutions, both equations must have same slope and y-intercept.

Hence, compare the coefficients:

`\displaystyle \large{\begin{cases} -(2)/(3)=-(4)/(k) \\ (5)/(3) = (10)/(k) \end{cases}}\\\\\displaystyle \large{\begin{cases} -2k=-12 \\ 5k = 30 \end{cases}}`

In the end, the value of k is still 6.