Question

A steel rolling mill can produce I-beams at the rate of 20 tons per week. Customer demand for the beams is 5 tons per week. To produce the I-beams, the mill must go through a setup that requires changing to the required rolling patterns. Each setup costs the mill $10,000 in labor and lost production. The I-beam cost the mill $2,000 per ton and has an inventory holding rate of 25 percent. Assume the plant operates for 50 weeks in a year. Using Microsoft Excel, calculate the following:

a) the optimal production batch size of the mill.
b) The maximum (highest) inventory level at the plant
c) The annual inventory holding cost
d) The annual setup cost of the plant
e) The annual product cost f) Total Annual Inventory Cost (TAIC)

Answer 1

A) 114 tons

C) $22800

D) $22807.02

Step-by-step explanation:

Given Data:

annual holding cost (H) = 25% * $2000

setup cost (s) = $10000

production rate = 20

weekly demand = 5 tons

first we have to calculate the Annual demand , holding cost and the usage rate:

Annual demand = 5 tons * 52 weeks

= 260 tons

Holding cost (H) = 25% * $2000

= $500

Usage rate = (production rate) / (customer demand)

= 20 / 5 = 4 tons

A) Optimal production batch size of the mill

Qp =
`\sqrt{(2DS)/(H) } * \sqrt{(P)/(P-u) }`

=
`\sqrt{(2*260*10000)/(500) } * \sqrt{(20)/(20-4) }`

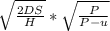
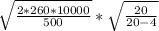
= 114 tons

C) The annual inventory holding cost

Annual holding cost

=
`(Imax)/(2) * H`

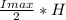
Imax = ( Qp / P ) (p-u)

= (114 / 20 ) ( 20 - 4 )

= 91.2 tons

therefore Annual holding cost : = ( 91.2 / 2) * 500 = $22800

D) Annual setup cost of the plant

=
`(D)/(Qp) * S`

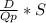
D = 260

Qp = 114

S = $10000

hence Annual setup cost of the plant

= (260/114) * 10000

= $22807.02