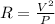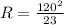Answer:
a

b
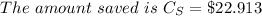
c
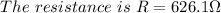
Step-by-step explanation:
From the question we are told that
The power used by incandescent bulb
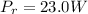
The power used by Compact fluorescent bulb
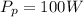
The life span of Compact fluorescent bulb is
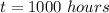
The prices of Compact fluorescent bulb is
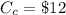
The prices of incandescent bulb is
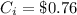
The life span of incandescent bulb is
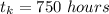
The cost of electricity is

The duration of daily bulb usage is
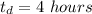
Generally 3 years of bulb usage in hours is mathematically evaluated as

=>

=>
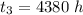
Generally the cost to power a 23W bulb for the above duration is mathematically represented as

=>

=>
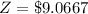
The number of Compact fluorescent bulbs required to achieve this about of time is mathematically represented as
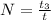
=>

=>
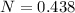
=>

The total cost of usage for the Compact fluorescent bulb is mathematically represented as
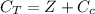
=>
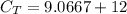
=>
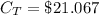
The number of incandescent bulbs required to achieve this about of time is mathematically represented as

=>
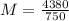
=>
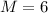
Generally the cost to power a 100W bulb for the above duration is mathematically represented as
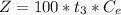
=>
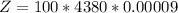
=>

The total cost of usage for the incandescent bulbs is mathematically represented as
![C_t = C_e + [6 *C_i]](https://img.qammunity.org/2021/formulas/physics/college/zw64no4zkz6lzma4rb28fc6mk17ffxlxhx.png)
=>
![C_t = 39.42 + [0.76 * 6]](https://img.qammunity.org/2021/formulas/physics/college/hs149dwwyf0w14ua0mxz5o7g2bac36oe4w.png)
=>

Generally the total amount saved is mathematically represented as

=>
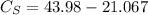
=>

Generally the resistance of the Compact fluorescent bulb is