Question

Two chemicals A and B are combined to form a chemical C. The rate, or velocity, of the reaction is proportional to the product of the instantaneous amounts of A and B not converted to chemical C. Initially, there are 100 grams of A and 50 grams of B, and for each gram of B, 2 grams of A is used. It is observed that 10 grams of C is formed in 7 minutes. How much is formed in 28 minutes? (Round your answer to one decimal place.) grams What is the limiting amount of C after a long time? grams How much of chemicals A and B remains after a long time? A grams B grams At what time is chemical C half-formed? t = min

Answer 1

Follows are the solution:

Step-by-step explanation:

A + B = C

Its response decreases over time as well as consumption of a reactants.

r = -kAB

during response A convert into 2x while B convert into x to form 3x of C

let's y = C

y = 3x

Still not converted sum of reaction

for A: 100 - 2x

for B: 50 - x

Shift of x over time

`(dx)/(dt) = (-k(100 - 2x))/((50 - x))`

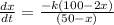
Integration of x as regards t

`(1)/([(100 - 2x)(50 - x)]) dx = -k dt\\\\(1)/(2[(50 - x)(50 - x)]) dx = -k dt\\\\\ integral\ (1)/(2[(50 - x)^2]) dx =\ integral [-k ] \ dt\\\\(-1)/([100-2x]) = -kt + D \\\\`

D is the constant of integration

initial conditions: t = 0, x = 0

`(-1)/([100-2x]) = -kt + D \\\\( -1)/([100]) = 0 + D\\\\D= (-1)/(100)\\\\`

hence we get:

`(-1)/([100-2x])= -kt -(1)/(100)\\\\or \\\\ (1)/((100-2x)) = kt + (1)/(100)`

after t = 7 minutes ,
`C = 10 \ g = 3x`

`3x = 10\\\\x = (10)/(3)`

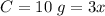
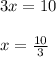
Insert the above value x into
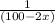`(1)/((100-2x))` equation
`= kt + (1)/(100)` to get k.

`\to (1)/((100-2* (10)/(3))) = k * (7) + (1)/(100) \\\\ \to (1)/((100- 2 * 3.33)) = (700k + 1)/(100) \\\\ \to (1)/((100-6.66)) = (700k + 1)/(100)\\\\ \to (1)/(93.34) = (700k + 1)/(100) \\\\`

`\to 100 = 93.34(700k + 1) \\\\ \to 100 = 65,338k + 700 \\\\ \to 65,338k = -600 \\\\ \to k = (-600)/( 65,338) \\\\ \to k= - 0.0091`

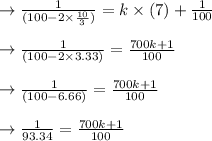
therefore plugging in the equation the above value of k

`\to (1)/((100-2x)) = kt +(1)/(100) \\\\\to (1)/((100-2x)) = -0.0091t + (1)/(100)\\\\\to (1)/((100-2x)) = (1 -0.91t)/(100)\\\\\to (1)/(2(50-x)) = (1 -0.91t)/(100)\\\\\to (1)/((50-x)) = (1 -0.91t)/(50)\\\\\to 50= (1-0.91t)(50-x)\\\\\to 50 = 50-45.5t-x-0.91tx\\\\\to x+0.91xt= -45.5t\\\\\to x(1+0.91t)= -45.5t\\\\\to x=(-45.5t)/(1+0.91t)`

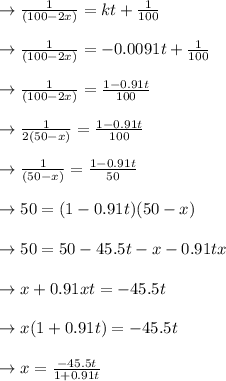
Let y = C

, calculate C:

y = 3x

`y =3 * (-45.5t)/(1+0.91t)`

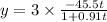
amount of C formed in 28 mins

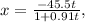`x = (-45.5t)/(1+0.91t) ,` plug t = 28

`\to x = (-1274)/(1+25.48) \\\\\to x = (-1274)/(26.48) \\\\\to x= -48.26`

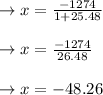
therefore amount of C formed in 28 minutes is = 3x = 144.78 grams

C:
`y =3 * (-45.5t)/(1+0.91t)`

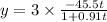
y= 136.5 =137