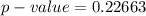Question

A ketchup company regularly receives large shipments of tomatoes. For quality control purposes, they take a sample of tomatoes from each shipment. If the sample shows convincing evidence that more than 8\%8%8, percent of the tomatoes in the entire shipment are bruised, then the company will request a new shipment of tomatoes. So the company tests H0 : p = 0.08 versus Ha ​: p > 0.08H, where p is the proportion of tomatoes in the entire shipment that are bruised.

One day, a supervisor takes a random sample of 600 tomatoes from a shipment and finds that 53 of the tomatoes are bruised, which results in a test statistic of z ≈ 0.75. Assuming that the necessary conditions are met, what is the approximate P-value associated with the significance test for this shipment?

Answer 1

P-value ≈ 0.2266

Explanation:

Answer 2

The value is
`p-value  =  0.22663`

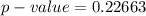
Explanation:

From the question we are told that

The proportion of bruised tomatoes p = 0.08

The null hypothesis is
`H_o  :   p =  0.08`

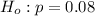
The alternative hypothesis is
`H_a  :  p >  0.08`

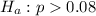
The sample size is n = 600

The number of bruised tomatoes from the sample selected is k = 53

The test statistics is z =0.75

Generally the p-value is mathematically represented as

`p-value  =  P(Z > z)`

=>
`p-value  =  P(Z > 0.75)`

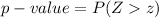
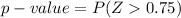
From the z-table

`P(Z > 0.75) =  0.22663`

So

`p-value  =  0.22663`