Question

Some transportation experts claim that it is the variability of speeds, rather than the level of speeds, that is a critical factor in determining the likelihood of an accident occurring (Update, Virginia Department of Transportation, Winter 2000). One of the experts claims that driving conditions are dangerous if the variance of speeds exceeds 75 (mph)2. On a heavily traveled highway, a random sample of 55 cars revealed a mean and a variance of speeds of 62.5 mph and 94.7(mph)2, respectively. (You may find it useful to reference the appropriate table: chi-square table or F table)

1. Set up the competing hypothesis to test wxpert,s claim.
2. At the 5% significance level find the critical value and state the decision rule.
3. Can you conclude that driving conditions are dangerous on this highway? explain.

Answer 1

Explained below.

Explanation:

The claim made by an expert is that driving conditions are dangerous if the variance of speeds exceeds 75 (mph)².

(1)

The hypothesis for both the test can be defined as:

H₀: The variance of speeds does not exceeds 75 (mph)², i.e. σ² ≤ 75.

Hₐ: The variance of speeds exceeds 75 (mph)², i.e. σ² > 75.

(2)

A Chi-square test will be used to perform the test.

The significance level of the test is, α = 0.05.

The degrees of freedom of the test is,

df = n - 1 = 55 - 1 = 54

Compute the critical value as follows:

`\chi^(2)_(\alpha, (n-1))=\chi^(2)_(0.05, 54)=72.153`

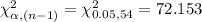
Decision rule:

If the test statistic value is more than the critical value then the null hypothesis will be rejected and vice-versa.

(3)

Compute the test statistic as follows:

`\chi^(2)=((n-1)* s^(2))/(\sigma^(2))`

`=((55-1)* 94.7)/(75)\\\\=68.184`

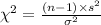
The test statistic value is, 68.184.

Decision:

`cal.\chi^(2)=68.184<\chi^(2)_(0.05,54)=72.153`

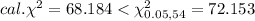
The null hypothesis will not be rejected at 5% level of significance.

Conclusion:

The variance of speeds does not exceeds 75 (mph)². Thus, concluding that driving conditions are not dangerous on this highway.